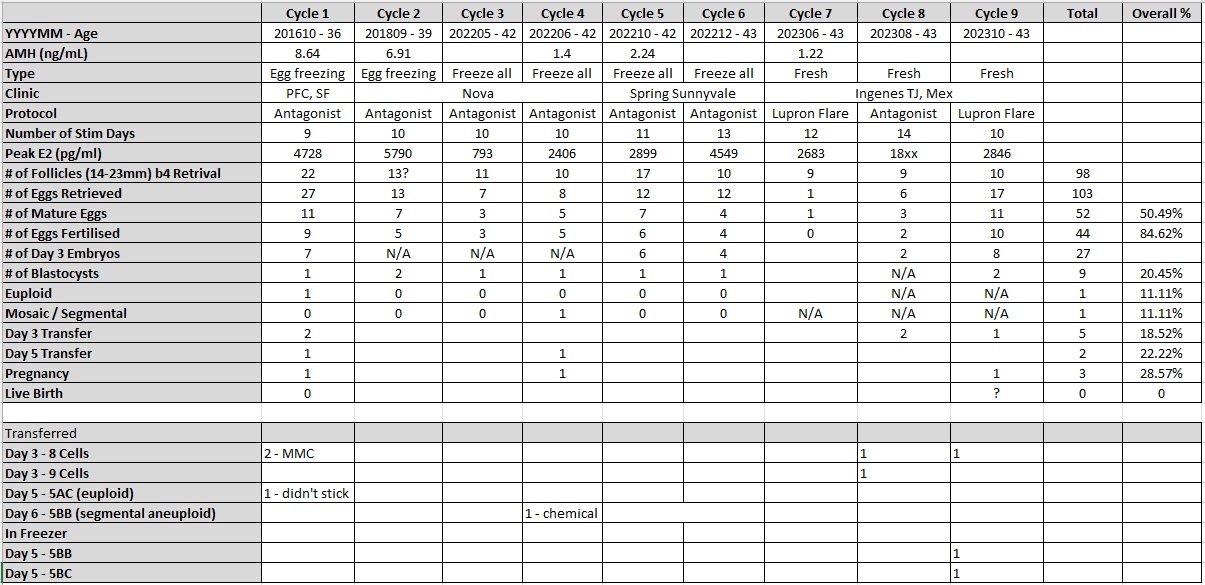
Principal Component Analysis (PCA) in R & Python
March 5, 2024
Hunger Game
# computer variance of principal components (sdev ^ 2)
pc_var <- prin_comp$sdev ^ 2
# calculate proportion of variance explainted by each pc
prop_varex <- pc_var / sum(pc_var)In Python
# Convert pandas df to numpy arrays
train_np = train_df[train_df.columns.difference(['label'])].values
test_np = test_df[test_df.columns.difference(['label'])].values
# Scale the values
from sklearn.preprocessing import scale as sklearnScale
train_scale = sklearnScale(train_np)
test_scale = sklearnScale(test_np)
# train PCA
from sklearn.decomposition import PCA as sklearnPCA
pca = sklearnPCA(n_components=train_df.shape[1]-1)
pca.fit(train_scale)
# calculate proportion of variance explained by each PC
var = pd.DataFrame({'PC': np.arange(1,train_df.shape[1]), 'var': np.round(pca.explained_variance_ratio_, decimals=4)*100})
# calculate the cumulative variance explained by each PC
cumvar = pd.DataFrame({'PC': np.arange(1,train_df.shape[1]), 'cumvar': np.cumsum(np.round(pca.explained_variance_ratio_, decimals=4)*100)})The first pc explains 21% variance, second pc explains 18% variance and so on…
Determine the number of principal components to model
In R
par(mfrow = c(1, 2))
plot(prop_varex, xlab="Principal Component", ylab="Proportion of Variance Explained", type="b", main="Scree plot")
plot(cumsum(prop_varex), xlab="Principal Component", ylab="Cumulative Proportion of Variance Explained", type="b", main="Cumulative Scree plot")In Python
import matplotlib.pyplot as plt
import seaborn as sns
fig, ax = plt.subplots(1,2,figsize=(10,5))
sns.pointplot(x="PC", y="var", data=var, ax=ax[0])
ax[0].title.set_text('Scree plot')
sns.pointplot(x="PC", y="cumvar", data=cumvar, ax=ax[1])
ax[1].title.set_text('Cumculative Scree plot')
display(fig.figure)The plot shows that 10 pc results in variance close to 97%, PCA reduces 18 predictors to 10 without compromising on explained variance
PCA transforms train and test dataset
Apply PCA transformation to the test dataset including the center and scaling feature
In R
# add training set with principal components
train_data <- data.frame(label = nc_train$label, prin_comp$x)
# select the first 10 PCs
train_data <- train_data[, 1:11]
# transform test dataset into PC
test_data <- predict(prin_comp, newdata = nc_test[, !(colnames(nc_test) %in%
c("label"))])
# select the first 10 PCs
test_data <- as.data.frame(test_data[, 1:10])In Python
# select the first 10 PCs
pca_reduced = sklearnPCA(n_components=10)
pca_reduced.fit(train_scale)
train_reduced_df = pd.DataFrame(pca_reduced.fit_transform(train_scale))
# add training set with principal components
train_reduced_df['label'] = train_df['label']
# transform test dataset into PC
test_reduced_df = pd.DataFrame(pca_reduced.fit_transform(test_scale))Predictive model with PCA Components
Use PCA components to train generalized linear models (binomial)
In R
# run a logistic model
train_control <- trainControl(method = "repeatedcv", number = 5)
glm_model <- train(label ~ ., data = train_data, method = "glm", family = binomial,
trControl = train_control)
# make prediction
test_data$pred <- predict(glm_model, newdata = test_data, type = "raw")
test_data$pred <- ifelse(test_data$pred > 0.5, 1, 0)
confusionMatrix(test_data$pred, nc_test$label)## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 212 3
## 1 3 31
##
## Accuracy : 0.9759
## 95% CI : (0.9483, 0.9911)
## No Information Rate : 0.8635
## P-Value [Acc > NIR] : 7.627e-10
##
## Kappa : 0.8978
## Mcnemar's Test P-Value : 1
##
## Sensitivity : 0.9860
## Specificity : 0.9118
## Pos Pred Value : 0.9860
## Neg Pred Value : 0.9118
## Prevalence : 0.8635
## Detection Rate : 0.8514
## Detection Prevalence : 0.8635
## Balanced Accuracy : 0.9489
##
## 'Positive' Class : 0
## In Python
# Run a logistic model
from sklearn.linear_model import LogisticRegression
glm = LogisticRegression()
glm.fit(train_reduced_df.iloc[:,:-1], train_reduced_df.iloc[:,-1])
# make prediction
test_reduced_df['pred'] = glm.predict(test_reduced_df)
from sklearn.metrics import confusion_matrix
print confusion_matrix(test_df['label'], test_reduced_df['pred'])## [[175 32]
## [ 23 19]]